My research focuses on leveraging multiple computer models with varying levels of fidelity (in terms of accuracy and cost) to achieve more accurate estimations, a field known as multi-fidelity (MF) modeling.

Motivation: Naval ship motion application (and especially their extremes)

Goal: Development of theoretically rigorous statistical methodologies

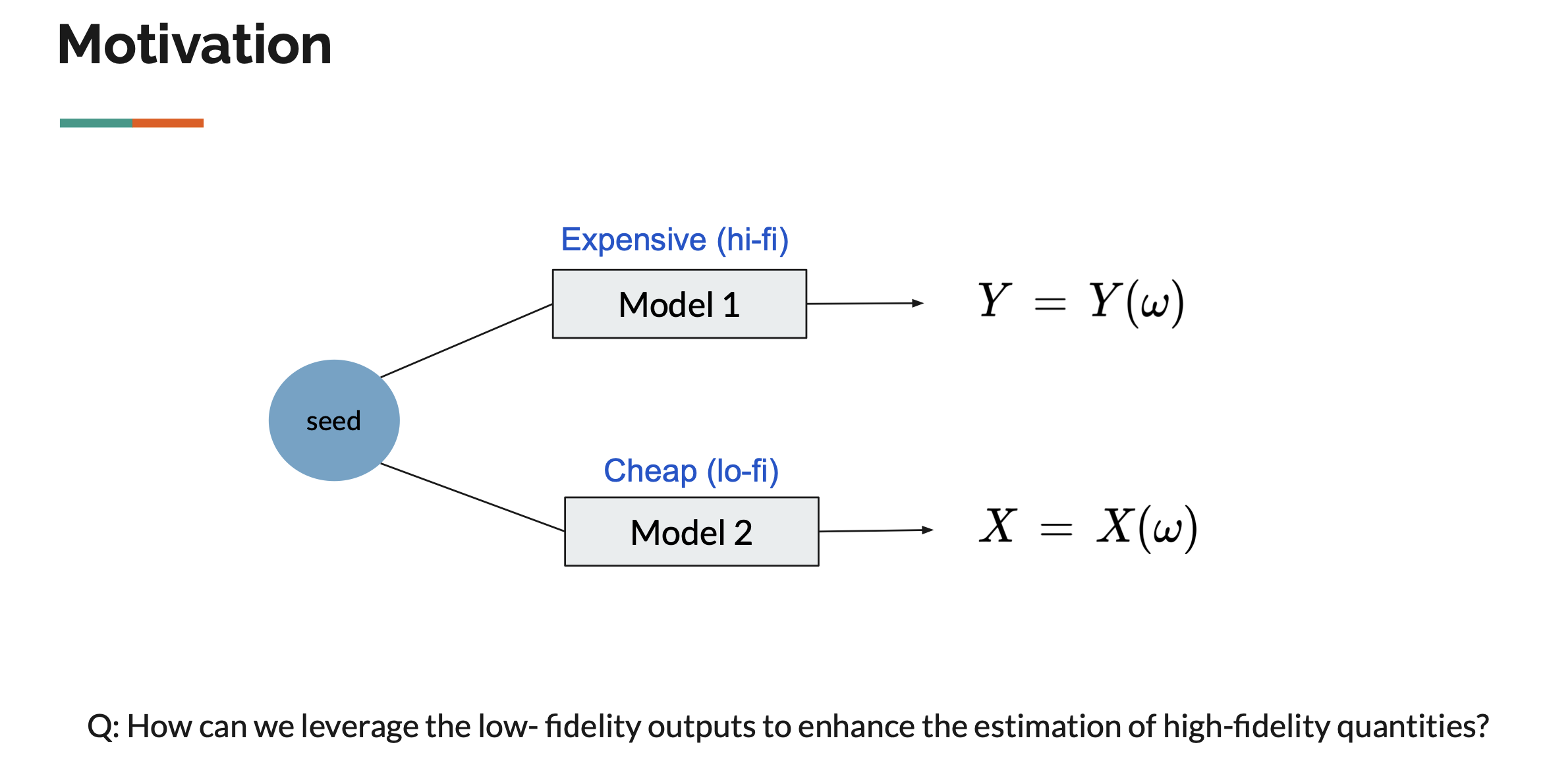
The ultimate goal of this research is to achieve probability density estimation of high-fidelity (expensive) outputs by effectively leveraging (cheap) surrogate model outputs. The research explores methods to address this challenge through:

1. Nonparametric kernel density estimation with importance sampling (Kim (2024a)).
2. Parametric ensemble estimator approach (Kim (2024b)).

The field includes semi-supervised learning problems, where we are given partially labeled data \((X_1,Y_1), \dots (X_n,Y_n), X_{n+1}, \dots, X_{n+m},\) as low-fidelity data ($X$) is more accessible than high-fidelity data ($Y$). According to Peherstorfer et al. (2018), MF strategies can be categorized into three types as follows:

1. Adaptation: High-fidelity information is used to enhance the lower-fidelity model.
2. Filtering: The low-fidelity model is explored to determine where to evaluate the high-fidelity model.
3. Fusion: This involves the combined use of multiple models.

My Contributions

The application of our interest concerns modeling ship motions (and especially their extremes) in the field of Naval Architecture. I have conducted a series of studies in this area, and my research can be categorized as follows:

• MF Calibration: Kim (2023) of adaptation type focused on improving the low-fidelity output by leveraging high-fidelity output.
• MF Importance Sampling: Kim (2024a) tackled the problem of estimating the probability density function (p.d.f) of high-fidelity values based on a kernel-based importance sampling estimator, a problem that combines filtering and fusion strategies.
• MFMC: Kim (2024b) research proposed an ensemble approach for parameter estimation in parametric distributions for multi-fidelity outputs. We propose and compare fusion-type multi-fidelity Monte Carlo estimators.

I also presented parts of this research during the Graduate Student Seminar at UNC Chapel Hill and my dissertaion proposal. You can find the slides here.

For more details, please refer to the corresponding publications.

References

• Peherstorfer, B., Willcox, K., and Gunzburger, M, (2018), ‘Survey of multifidelity methods in uncertainty propagation, inference, and optimization’. SIAM Review, 60(3), 550–591.

• M. Kim, V. Pipiras, A. Reed, K. Weems, (2023), Calibration of low-fidelity ship motion programs through regressions of high-fidelity forces, Ocean Engineering, 290, 116321

• M. Kim, K. O’Connor, V. Pipiras, T. Sapsis, (2024a), Sampling low-fidelity outputs for estimation of high-fidelity density and its tails, SIAM/ASA Journal on Uncertainty Quantification, to appear

• M. Kim, B. Brown, V. Pipiras, (2024b), Parametric multi-fidelity Monte Carlo estimation with applications to extremes, Preprint.