Another area of my research focuses on using coordinate-based neural networks for data-driven and physics-informed learning to approximate solutions of spatio-temporal governing PDEs.

Motivation: Solve spatio-temporal parametrized partial differential equations (PDEs).

Goal: Introducing a physics-informed learning objective to the latent state modeling structure

• Latent state projection via decoder-only process using implicit neural representation.
• Latent dynamics modeled using parametric neural ODEs (PNODEs).

CNF-ROM Structure

• Objective: Learn coordinate-based NN to approximate parameterized PDE solution.
• The approach combines a parametric neural ODE (PNODE, Lee and Parish 2021), which models latent dynamics, with a decoder that reconstructs PDE solutions.
• The decoder maps the latent state and coordinates to the solution (Yin et al., 2023), while the PNODE captures distinct latent trajectories for each parameter.

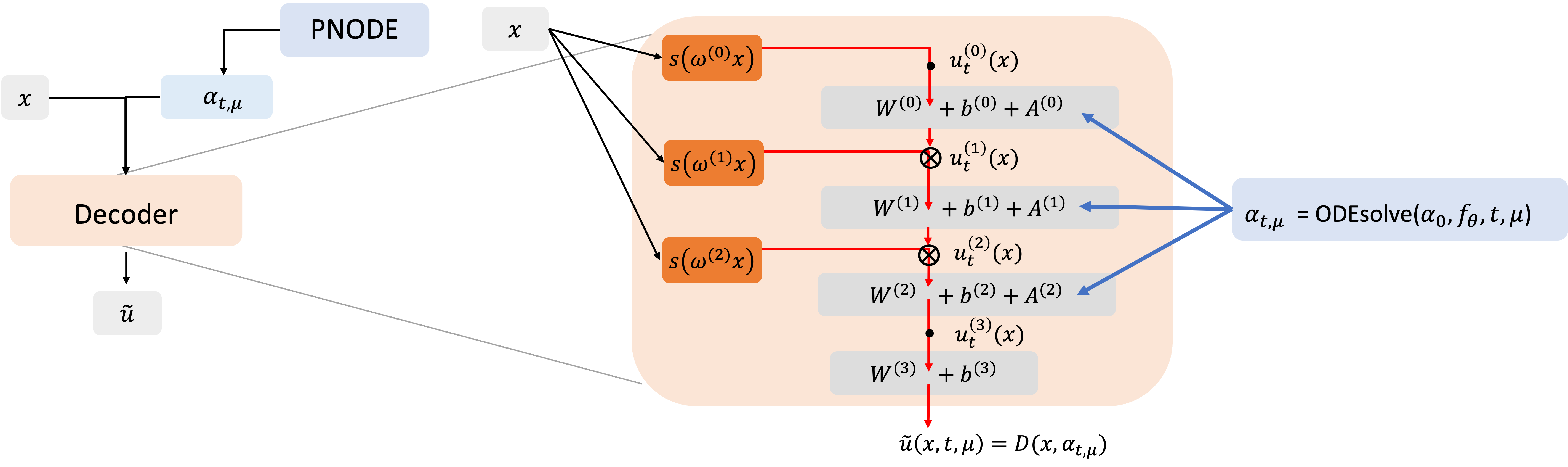
PINNs Objective

• PDE residual loss is available for CNF-ROM.
• The CNF-ROM leverages coordinate-based neural networks to directly compute spatial derivatives via automatic differentiation.
• Temporal dynamics, on the other hand, are modeled through a latent state $\alpha_{t,\mu}$ that evolves over time for each $\mu$. Using the chain rule, temporal derivatives are expressed as:

\[\frac{\partial D(x, \alpha)}{\partial t} = \frac{\partial D}{\partial \alpha} f( \alpha, \mu, t)\]

• Instead of incorporating IC and BC as loss terms, we address strategies for imposing exact IC and BC and discuss the trade-offs in this approach in the following paragraphs.

---

Trade-offs in Imposing Exact IC/BC

1. Limitation of Physics-informed Neural Networks (PINNs)
   • Initial and boundary conditions (IC, BC) are not strictly met when added as loss terms.
   • Introduced: Approximate distance function to impose hard constraints.
2. Limitation of R-function-based Approximate Distance Function (ADF, $\phi$, Sukumar and Srivastava 2022)
   • The second and higher-order derivatives of $\phi$ explode at the joining points or boundaries.
   • Introduced an auxiliary CNF-ROM to learn the first derivatives of the model ouput to replace second or higher-order derivatives with the derivatives of the auxiliary network.

---

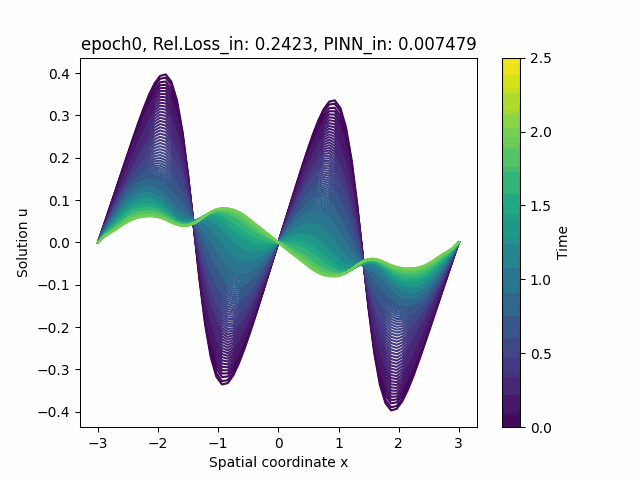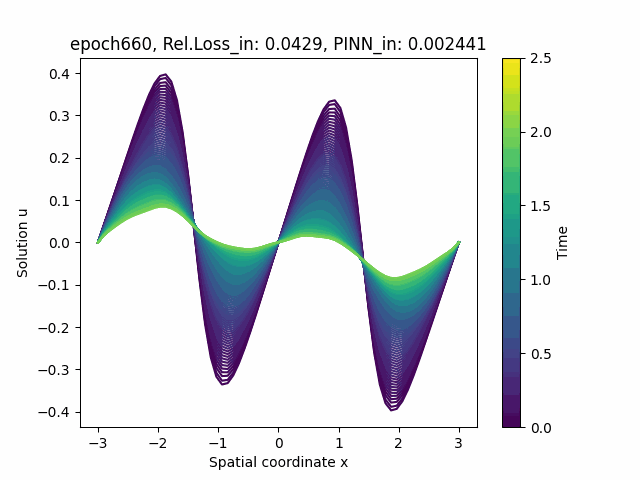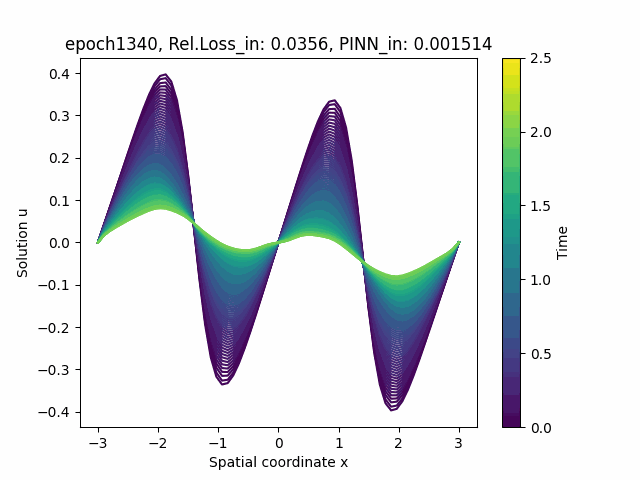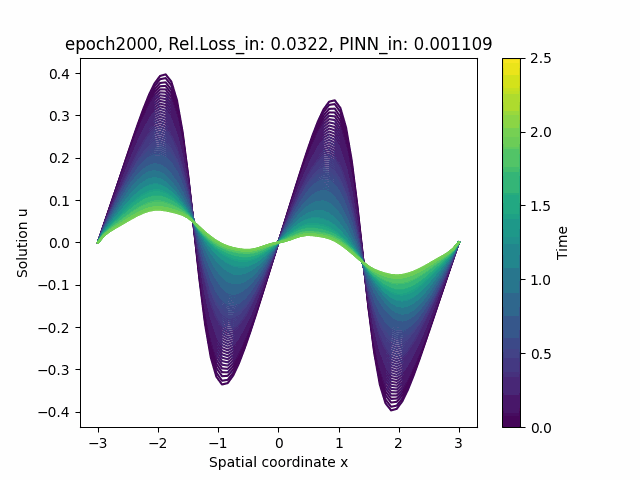
References

• M. Kim, T. Wen, K. Lee, Y. Choi, (2024), Physics-informed reduced order model with conditional neural fields, NeurIPS 2024 Workshop on Machine Learning and the Physical Sciences, (to appear).

• K. Lee and E. J. Parish, (2021), Parameterized neural ordinary differential equations: applications to computational physics problems, Proceedings of the Royal Society A, 477(2251):20210162.

• Y. Yin, M. Kirchmeyer, J. Franceschi, A. Rakotomamonjy, and P. Gallinari, (2023), Continuous PDE dynamics forecasting with implicit neural representations, In The Eleventh International Conference on Learning Representations.

• N. Sukumar and A. Srivastava, (2022), Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks, Computer Methods in Applied Mechanics and Engineering, 389:114333.